Suppose there is a riskless financial asset that costs one dollar at the beginning of the period and pays $1 + r$ dollars at the end of every period. The difference, $r$, is taxed at rate $t$.

Thus, it is possible to borrow and lend at the after-tax rate of $r(1 - t)$ per period. There is also a real asset costing $x > 0$. The asset produces a riskless pretax cash flow of $k$ in perpetuity at the end of each period.

For tax purposes, the original cost of the asset may be depreciated straight line at rate $0 \leq d \leq 1$. Taxable income for any period is the pretax cash flow less the depreciation.

But wait!?!? Didn’t you just tell us not to consider depreciation?

Tax is paid at rate $t$, so that at the end of the first period, the net-of-tax cash flow is

\[k-t(k-dx)\]

Depreciation is impacting cash flow through it’s impact on taxes!

We can rewrite the net-of-tax cash flow equation above as follows:

\[k(1-t) + dtx\]

The cash outflow $x$ to acquire the asset is not tax deductible. Suppose further that other income is available to offset tax depreciation in excess of cash flows from the asset. Then the net present value of investing in the real asset is

\[-x + \sum^{1/d}_{n=1}\frac{k(1-t)+dtx}{[1+r(1-t)]^{n}}+\sum^{\inf}_{n=1+1/d}\frac{k(1-t)}{[1+r(1-t)]^{n}}\]

This quantity can be rewritten as follows. Each of the three components of this expression has a straightforward interpretation.

\[-x+\frac{k}{r}+\frac{dtx}{r(1-t)}\Big(1-[1+r(1-t)]^{-1/d}\Big)\]
  1. The first term is the cost of the asset again.
  2. The second term is the present value of the perpetual pre-tax cash flow from the asset, $k$, capitalized at the pre-tax rate, $r$. Note that this is the same as the after tax cash flow, $k(1-t)$, capitalized at the after tax discount rate, $r(1-t)$.
  3. The final term is the present value of the reduction in tax payments afforded by the depreciation deduction (often called the tax shield).1 This is the only term where tax factors $d$ and $t$ play a role.
    • If either the depreciation rate or the tax rate is zero, then the before tax and net-of-tax present values are the same.
    • If $d$ and $t$ are both positive then the value of the tax shield provided by depreciation is also positive. The value of the shield increases with both $d$ and $t$.
    • When tax depreciation is immediate, i.e., $d=1$, then the tax shield is
\[x\frac{t}{1+r(1-t)}\]

Notice that this term has the same form as the present value of an annuity of $dtx$ for $1/d$ periods discounted at rate $r(1-t)$.

Let’s do some plotting to get a sense of this relationship

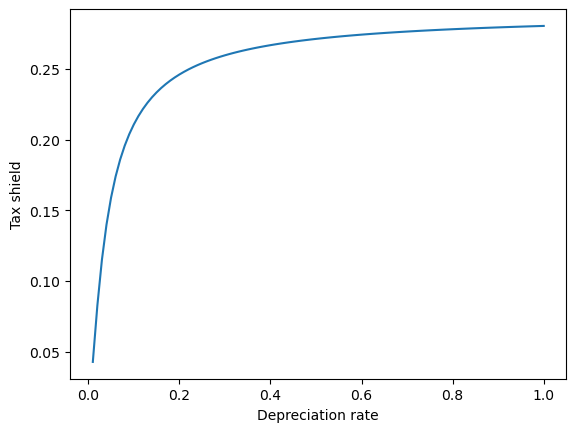
First let’s plot the value of the tax shield as a function of the depreciation rate.

Next let’s plot the value of the tax shield as a function of the tax rate.

Then lets look at the relationship in a spreadsheet.

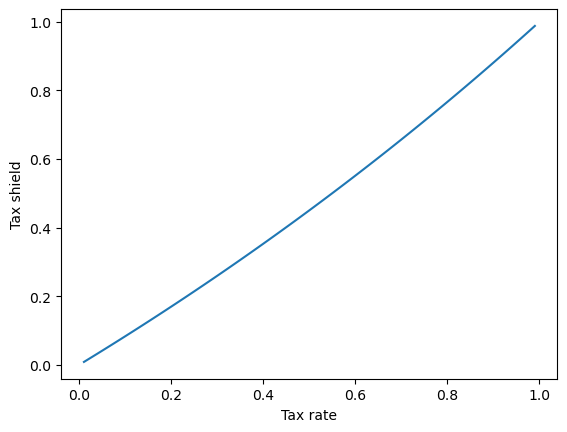
One surprising conclusion that might be drawn from this analysis is that the net-of-tax present value of an investment is increasing in t. That is, the higher the tax rate, the more attractive is the investment!

This is kind of the point!

Questions:

  1. The statement above is a striking one. What must be held constant (and probably is not in real life) for it to be true?
  2. What condition defines equilibrium prices and returns on financial assets relative to real assets?
  3. What opportunities would you be able to exploit if you observed that prices and returns were not in equilibrium?
  4. What effect would your actions tend to have on prices and returns?
  5. Tricky question. What happens to the value of the value of the depreciation tax shield as the tax rate, t approaches 100%? What is the intuition behind this result?

  1. ↩