Lecture 2: The Nature of Costs

ACCT 3210

Dr. Morris

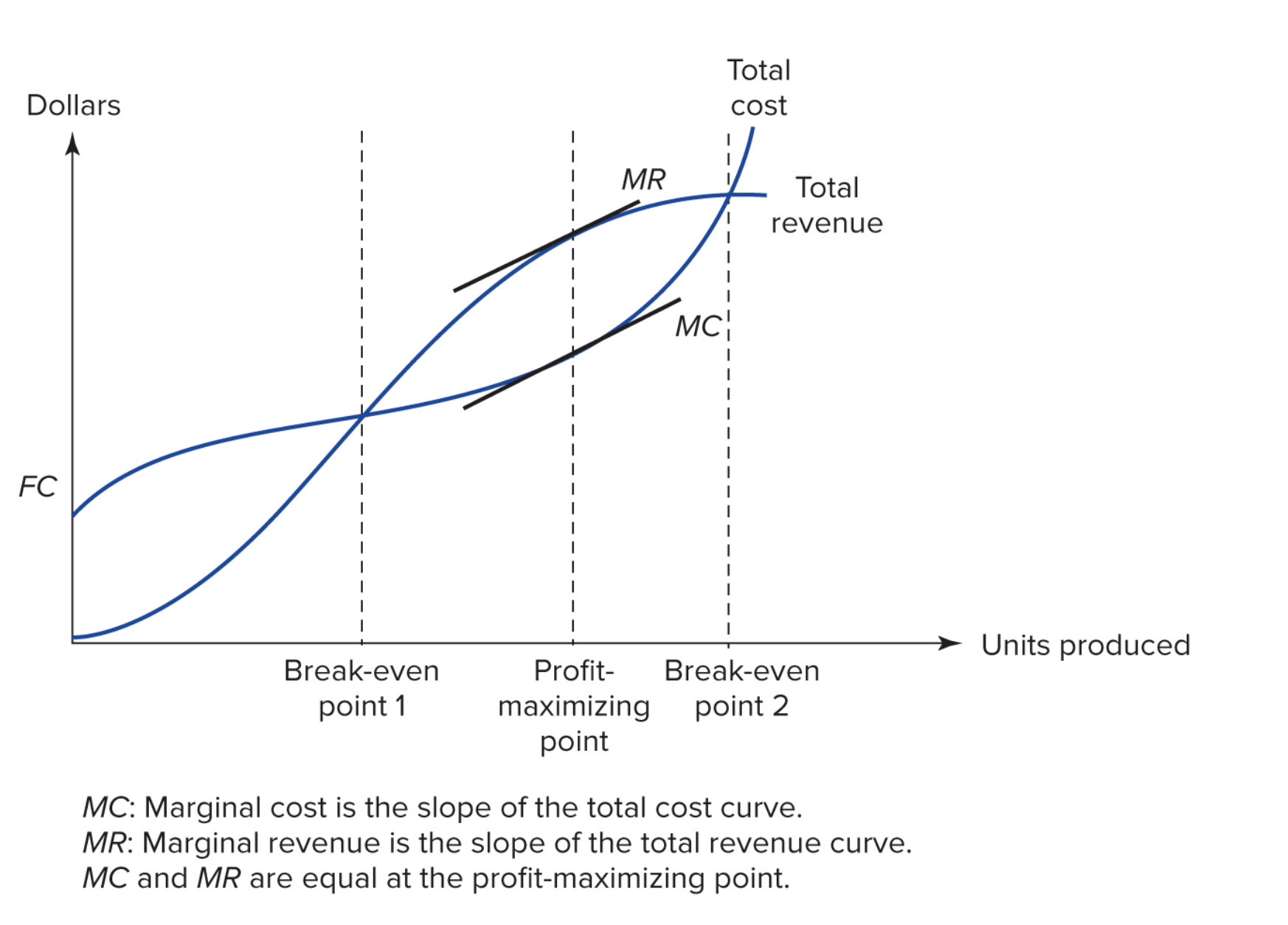
We are interested in how costs respond to business decisions? Why?

• Costs are resources. Business decisions that have costs require resources so we need to make sure we have the resources when required.
• Cost, Volume, Profit analysis. Which we will talk about in the following lectures, is based on the relationship between a key decision---the volume decision (how much to produce)---and costs.
• We have to know where the resources are and where they need to them to be in order to understand the resource bargins that need to be negotiated.

Why do we care about costs?

Profit = Revenue - Total Cost

Total Cost = Fixed Cost + $\sum$ (Cost Per Unit $\times$ # Units) ¹

Revenue = $\sum$ (Price Per Unit $\times$ # Units) ¹

^{1: Summed across all products.}

• Apple chooses how many devices to produce based projections of how costs and revenues will respond to this decision.²

• Today we will focus on modelling the cost portion of this equation.

^{2: All my examples are Apple. Sorry.}

Cost Functions

Models of the firm that we use to predict how cost will respond to various actions, which we express as variables in the model.

A simple example where everything is linear:

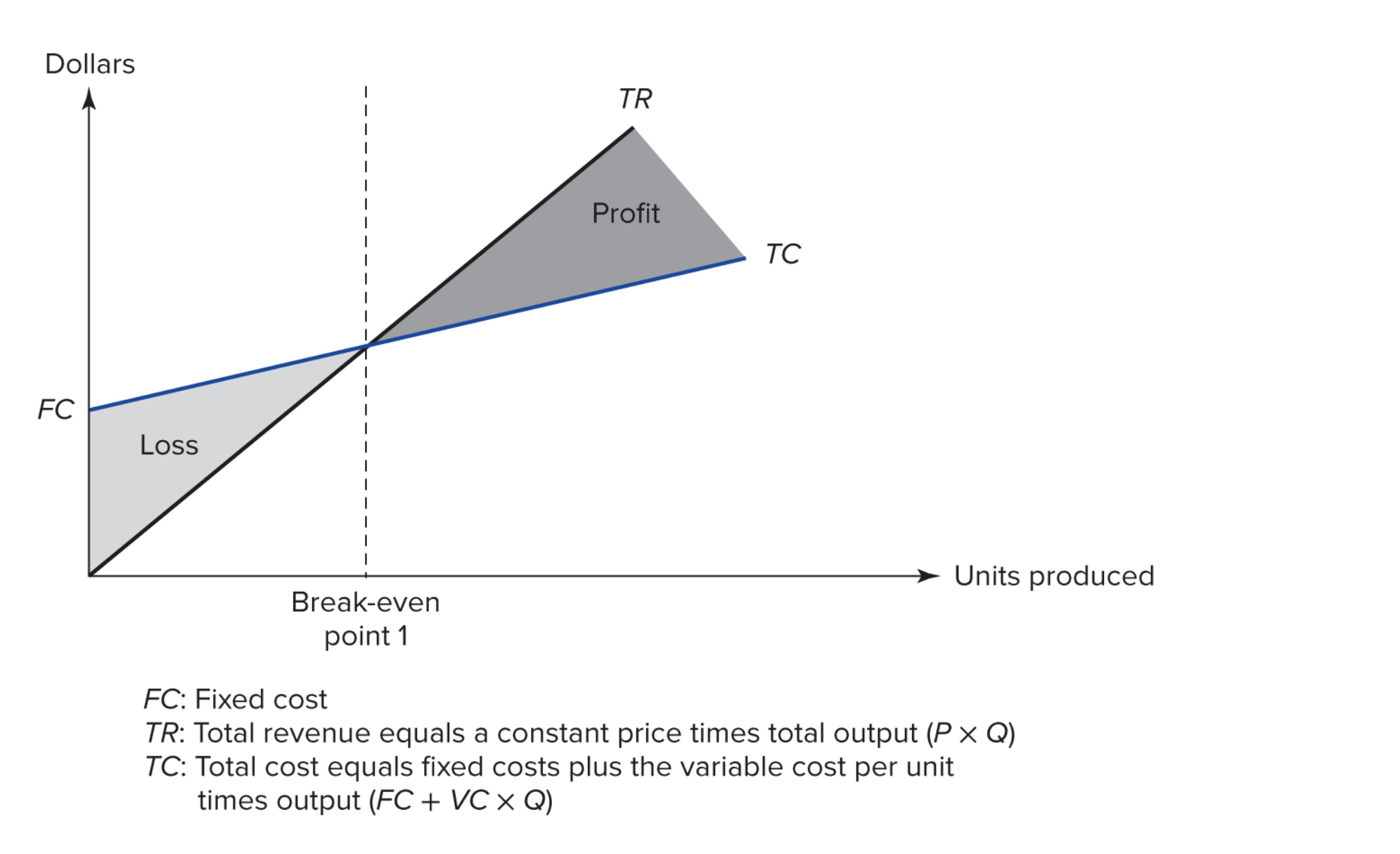
Let's look at some cost terms in the context of a single-product firm.

• Fixed cost (FC): Cost at zero output. Also used to refer to costs that do not vary with output (or some other driver).
• Variable cost (VC): Cost that vary with output (or some other driver).

• Marginal cost (MC): The cost per unit at the margin (i.e. the point of interest). This is the rate of change of cost at the margin.
• Incremental cost (IC): The cost of producing the next unit. Often MC and IC have the same value, but they are slightly different things!
• Average cost (ATC): Total Cost of producing the output over the number of units of output. This is a simple average for single product firms. It is not simple at all for multi-product firms.

iPRS here.

• Cost object: An activity or item for which we want to measure cost.
• Cost driver: Any factor or activity whose change leads to a change in costs.

A simple example where everything is linear:

Can you see anything unrealistic in this graph?

Most firms' costs are non-linear

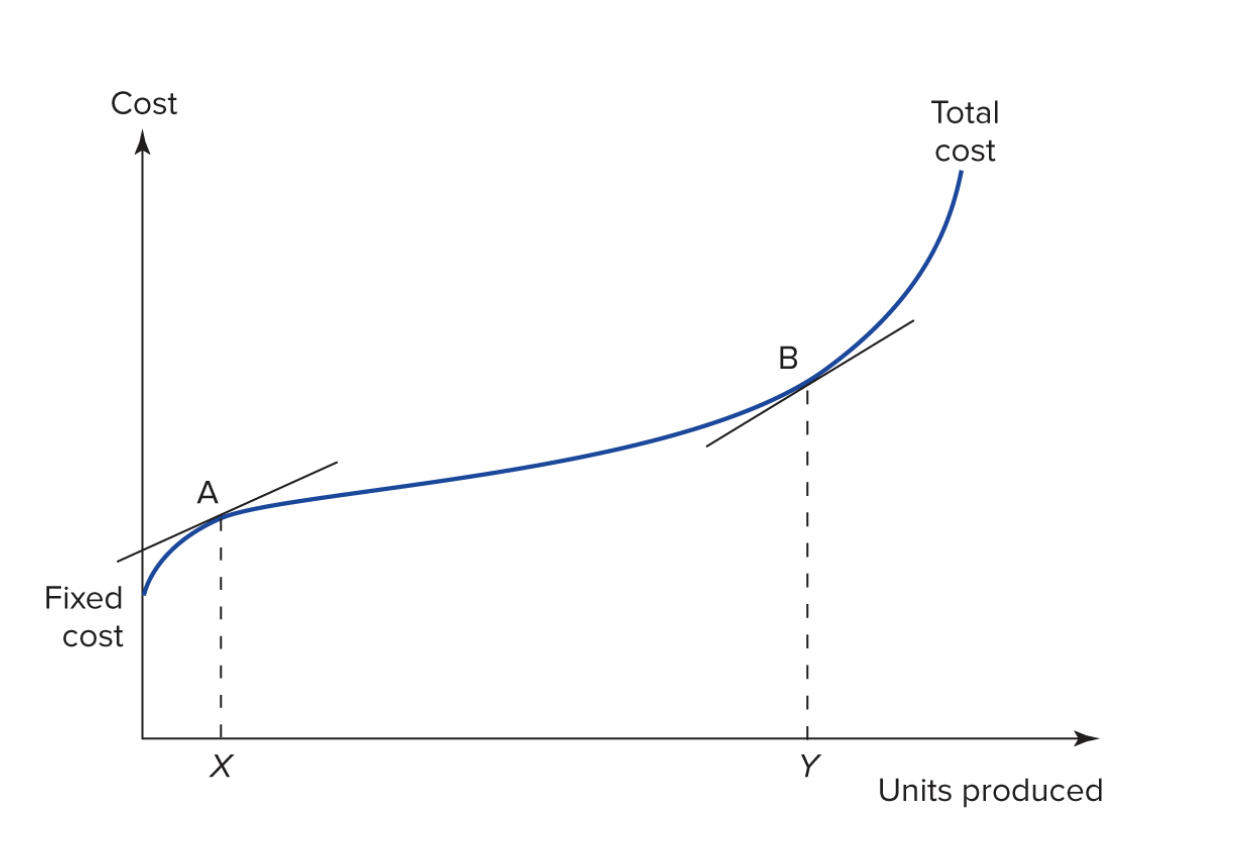
1. What is the economic significance of the area to the left of the line from X to A?
2. What is the economic significance of the area between X->A and Y->B?
3. What is the economic significance of the area to the right of Y->B?

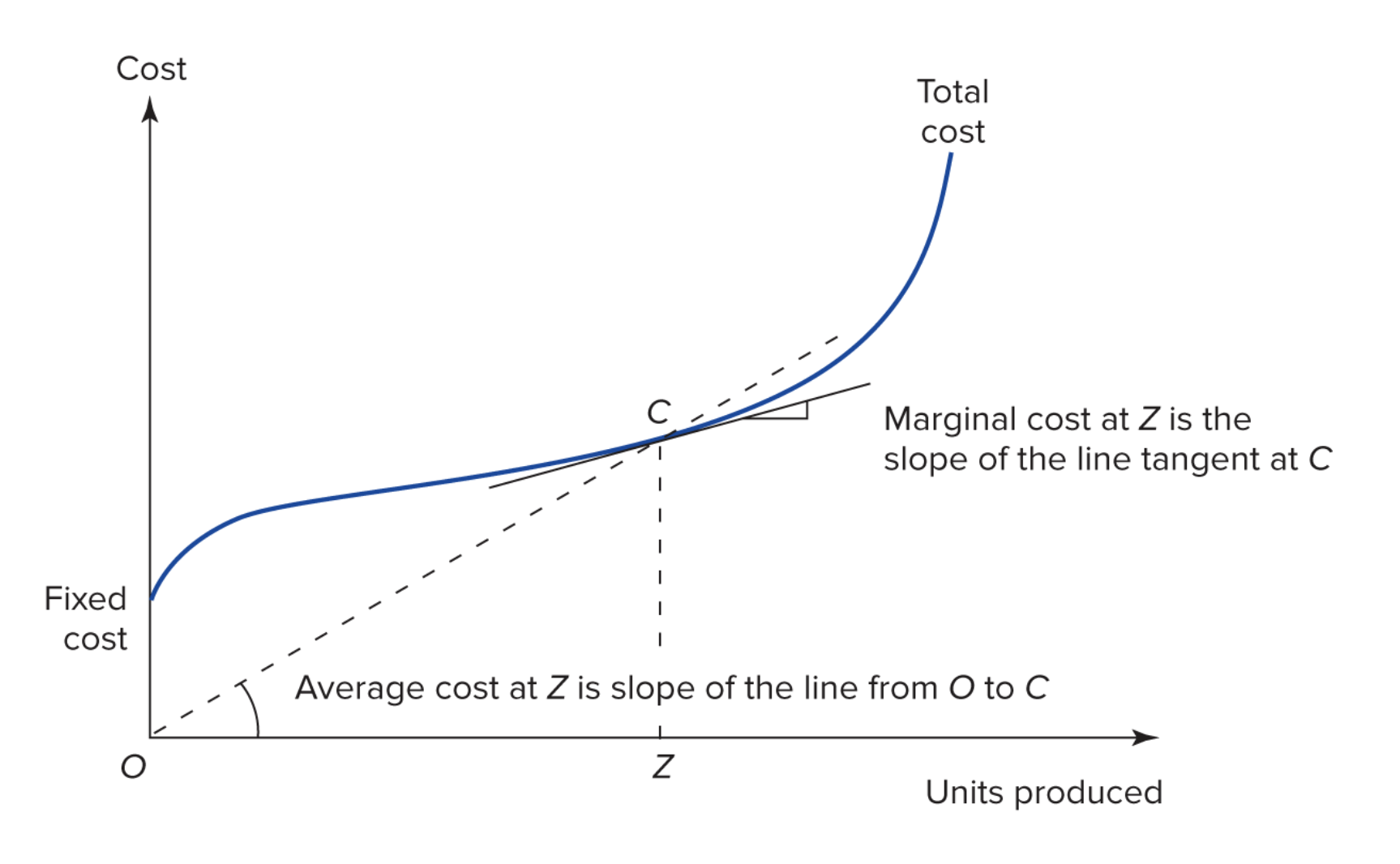
1. If marginal cost is the slope of the tangent line and incremental cost is the cost of one unit, then when are they the same on this graph?
2. When are they different?

At any scale there is a range within which production is efficient

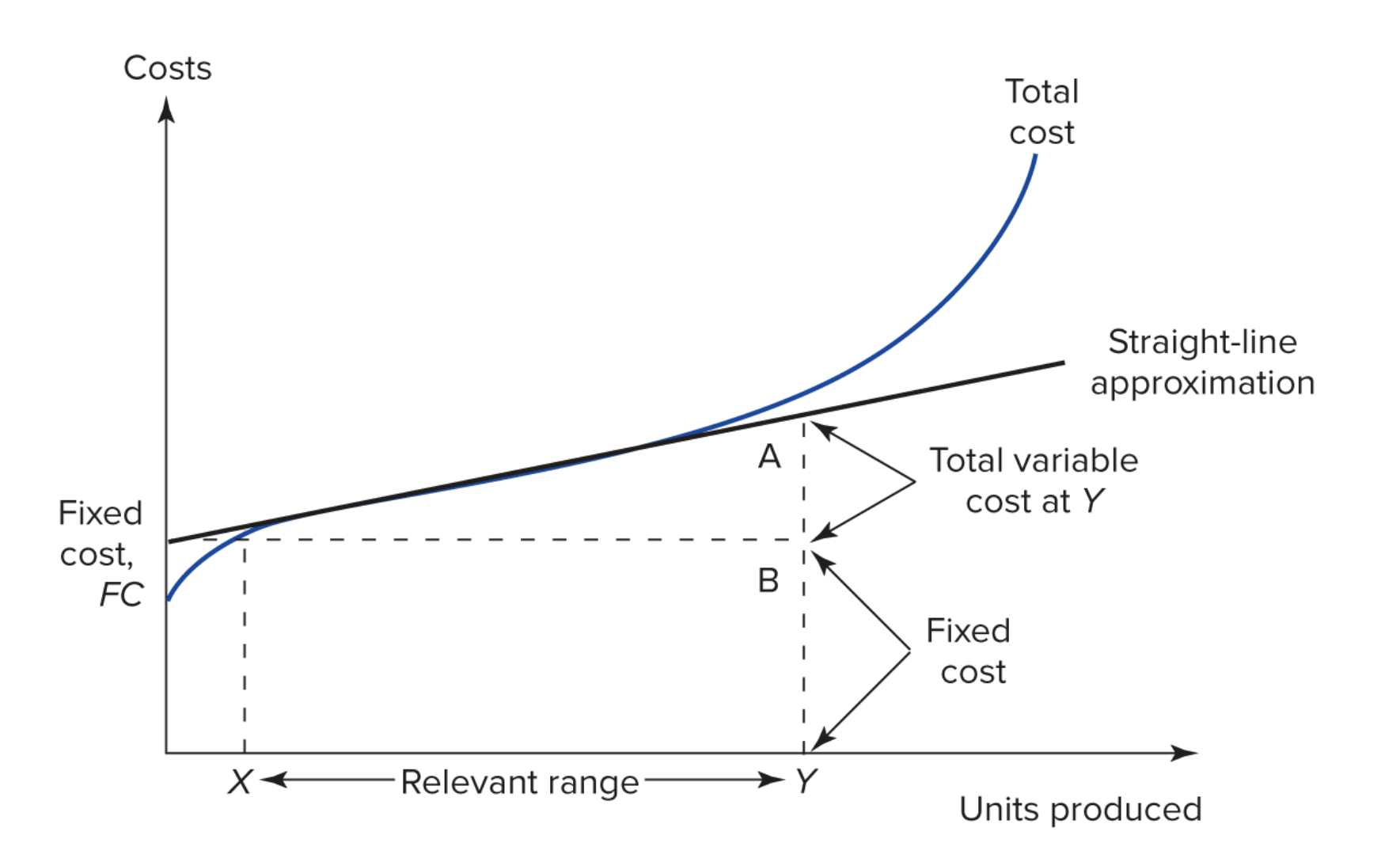
Producing outside of this range is less efficient, unless we change the scale of the firm.

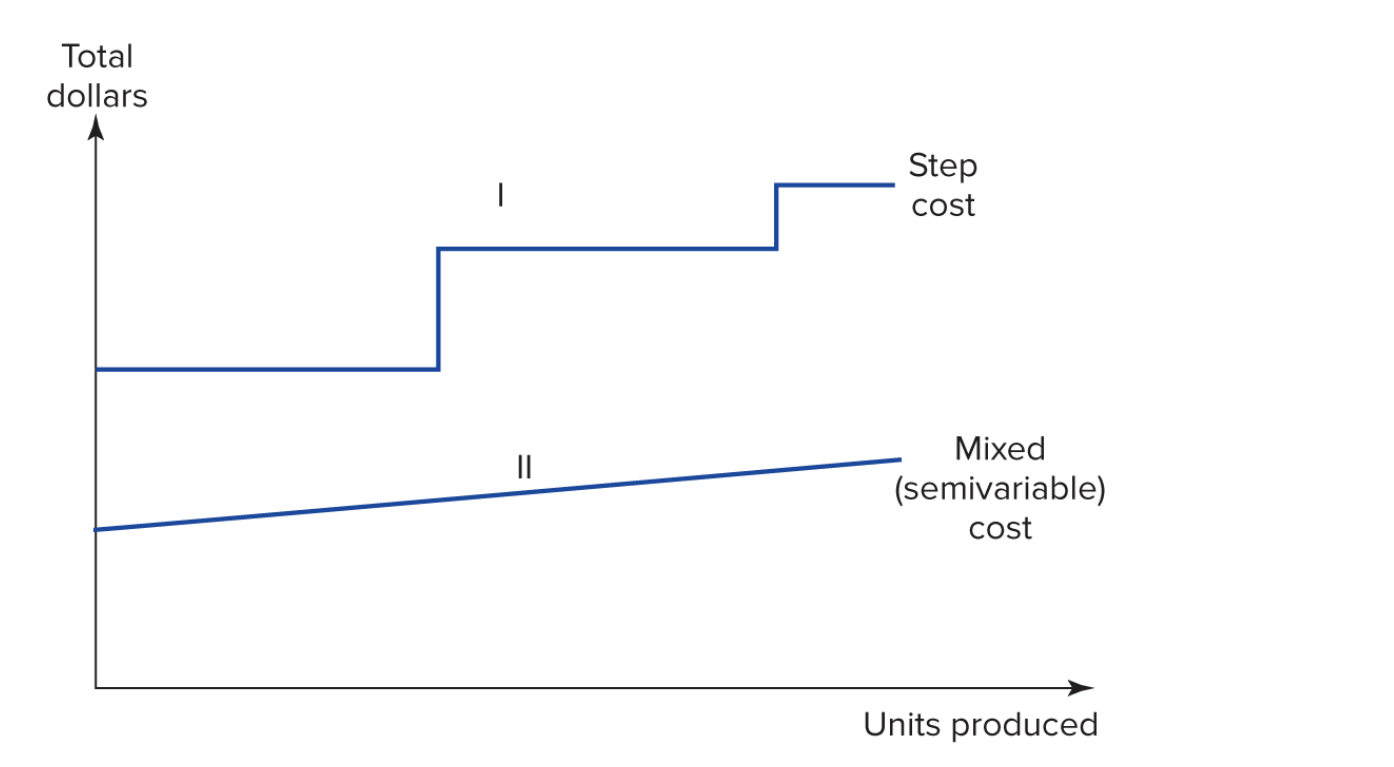
• Most firms have a mix of these attributes.
• Steps occur when the scale of the firm changes (e.g. we add a new factory).

Let's talk about the homework assignment!

• Download the Excel File here
• Please note that Python, Excel, or any other set of tools can be used on the homework!

Cost in a Multiproduct Firm:

Consider three firms that produce two products with quantities denoted $q_1$ and $q_2$. The three distinct cost functions are:

• $C_1(q_1, q_2) = 10q_1 + 5q_2$
• $C_2(q_1, q_2) = 6q_1 + q_1^2 + 8q_2 + q_2^2$
• $C_3(q_1, q_2) = 7q_1 + 9q_2 + q_1q_2$

1. Fill in the following table for each of the cost functions. (Incremental cost refers to the incremental cost of one additional unit of output.)

Output	Total Cost	Average Cost	Marginal Cost	Incremental Cost
$q_1, q_2$		$q_1, q_2$	$q_1, q_2$	$q_1, q_2$
100, 50
60, 50
40, 50
30, 10
30, 50
30, 70

Total cost:

• Plug the output data into each cost function!

Let's fill this out using Python (don't panic), Excel (also don't panic).

We'll start with Excel

Reference items:

• Marginal cost (MC): The cost per unit at the margin (i.e. the point of interest). This is the rate of change of cost at the margin.
• Incremental cost (IC): The cost of producing the next unit. Often MC and IC have the same value, but they are slightly different things!
• Average cost (ATC): Total Cost of producing the output over the number of units of output. This is a simple average for single product firms. It is not simple at all for multi-product firms.
• $C_1(q_1, q_2) = 10q_1 + 5q_2$
• $C_2(q_1, q_2) = 6q_1 + q_1^2 + 8q_2 + q_2^2$
• $C_3(q_1, q_2) = 7q_1 + 9q_2 + q_1q_2$

Now Python

You can follow along in colab.

First we need to load some data science libraries:

# import pandas so we can put everything into a nice friendly data frame
import pandas as pd 
import numpy as np

# lets put what we know into a dict (python dicts are POWERFUL use them when in doubt)
outputs = {
    "q1" : [100, 60, 40, 30, 30, 30],
    "q2" : [50, 50, 50, 10, 50, 70],
}
outputs

{'q1': [100, 60, 40, 30, 30, 30], 'q2': [50, 50, 50, 10, 50, 70]}

Table for Firm 1

# use pandas to make that into a dataframe
cost_frame_1 = pd.DataFrame(outputs) 
cost_frame_2 = pd.DataFrame(outputs) 
cost_frame_3 = pd.DataFrame(outputs) 
cost_frame_1

	q1	q2
0	100	50
1	60	50
2	40	50
3	30	10
4	30	50
5	30	70

Next write down our cost functions as... well... functions

# write down our cost functions
## total cost
def cost_1(q1,q2):
    return 10 * q1 + 5 * q2 
def cost_2(q1,q2):
    return 6 * q1 + q1**2 + 8 * q2 + q2**2 # note that we have to use ** inplace of ^ here
def cost_3(q1,q2):
    return 7 * q1 + 9 * q2 + q1 * q2    

Notice how close this is to how you might type this on your phone!

Then we can use those functions to calculcate average cost

• We can just pass q1,q2 as arguements to the cost functions

cost_1(100,50)

1250

cost_2(100,50)

13500

cost_3(100,50)

6150

Now we need to do this to all the data in the data frames

slow simple way:

TotalCost1 = []
for q1,q2 in zip(outputs['q1'],outputs['q2']):
    TotalCost1.append(cost_1(q1,q2))
print(TotalCost1)
outputs

[1250, 850, 650, 350, 550, 650]

{'q1': [100, 60, 40, 30, 30, 30], 'q2': [50, 50, 50, 10, 50, 70]}

cost_1(100,50)

1250

less simple but faster way

TotalCost1 = [cost_1(q1,q2) for q1,q2 in zip(outputs['q1'],outputs['q2'])]
print(TotalCost1)

[1250, 850, 650, 350, 550, 650]

super fast way that scales to large datasets

cost_frame_1["Total Cost"] = np.vectorize(cost_1)(cost_frame_1['q1'],cost_frame_1['q2'])
cost_frame_1

	q1	q2	Total Cost
0	100	50	1250
1	60	50	850
2	40	50	650
3	30	10	350
4	30	50	550
5	30	70	650

# we can do this for the other to firms:
cost_frame_2["Total Cost"] = np.vectorize(cost_2)(cost_frame_2['q1'],cost_frame_2['q2'])
cost_frame_3["Total Cost"] = np.vectorize(cost_3)(cost_frame_3['q1'],cost_frame_3['q2'])
cost_frame_2

	q1	q2	Total Cost
0	100	50	13500
1	60	50	6860
2	40	50	4740
3	30	10	1260
4	30	50	3980
5	30	70	6540

Average cost

The average cost of a each product is the total cost for producing that product alone devided by the number of units produced.

For firm 1 & 2 this is straightforward, each firm has an AC for each product where we plug in zero for the other product:

• $AC_1(q_1) = (10q_1 + 0)/q_1$
• $AC_1(q_2) = (0 + 5q_2)/q_2$

• $AC_2(q_1) = (6q_1 + q_1^2 + 0 + 0)/q_1$
• $AC_2(q_2) = (0 + 0 + 8q_2 + q_2^2)/q_2$

What about firm 3?

$$C_3(q_1, q_2) = 7q_1 + 9q_2 + q_1q_2$$

What does $q_1\times q_2$ mean?

• when two products are multiplied like this we often refer to it as an "interaction"
• Plugging in zero no longer separates the costs.

• Calculating the average cost for each product requires us to separate the costs of the products.
• When there are interactions between products their costs are inseparable!!
• So "average cost" is no longer a meaningful number!

One way to think of this is that average cost requires us to pretend that the firm only produces one product. When we can separate costs then this pretend firm tells us something about the real firm. When we cannot separate costs, this pretend firm does not tell us anything about the real firm!!

One way to do this in python is to write a function

# avg cost by product
def avg_cost(cost_function,q1=0,q2=0):
    """
    cost_function: the cost function you are averaging
    pass either q1 or q2 but not both to tell which product to use
    """
    if q1!=0 & q2!=0:
        print("only pass one nonzero argument")
        return None
    else:
        return cost_function(q1,q2) / (q1+q2)

Firm 1

# average cost the fast way
cost_frame_1["Average Cost q1"] = np.vectorize(avg_cost)(cost_1,q1=cost_frame_1['q1'])
cost_frame_1["Average Cost q2"] = np.vectorize(avg_cost)(cost_1,q2=cost_frame_1['q2'])
cost_frame_1

	q1	q2	Total Cost	Average Cost q1	Average Cost q2	Marginal Cost q1	Marginal Cost q2	Incremental Cost q1	Incremental Cost q2
0	100	50	1250	10.0	5.0	10	5	10	5
1	60	50	850	10.0	5.0	10	5	10	5
2	40	50	650	10.0	5.0	10	5	10	5
3	30	10	350	10.0	5.0	10	5	10	5
4	30	50	550	10.0	5.0	10	5	10	5
5	30	70	650	10.0	5.0	10	5	10	5

Firm 2

# average cost the fast way
cost_frame_2["Average Cost q1"] = np.vectorize(avg_cost)(cost_2,q1=cost_frame_2['q1'])
cost_frame_2["Average Cost q2"] = np.vectorize(avg_cost)(cost_2,q2=cost_frame_2['q2'])
cost_frame_2

	q1	q2	Total Cost	Average Cost q1	Average Cost q2	Marginal Cost q1	Marginal Cost q2	Incremental Cost q1	Incremental Cost q2
0	100	50	13500	106.0	58.0	206	108	207	109
1	60	50	6860	66.0	58.0	126	108	127	109
2	40	50	4740	46.0	58.0	86	108	87	109
3	30	10	1260	36.0	18.0	66	28	67	29
4	30	50	3980	36.0	58.0	66	108	67	109
5	30	70	6540	36.0	78.0	66	148	67	149

Marginal Cost

The marginal cost is the derivative of the cost function wrt. the product.

$$C_1(q_1, q_2) = 10q_1 + 5q_2$$$$MC_1(q_1) = 10$$$$MC_1(q_2) = 5$$

$$C_2(q_1, q_2) = 6q_1 + q_1^2 + 8q_2 + q_2^2$$$$MC_2(q_1) = 6 + 2q_1$$$$MC_2(q_2) = 8 + 2q_2$$

$$C_3(q_1, q_2) = 7q_1 + 9q_2 + q_1q_2$$$$MC_3(q_1) = 7 + q_2$$$$MC_3(q_2) = 9 + q_1$$

• This might help with the intuition for the average cost in this case!

Hate Calculus?

let's make python do the work

# we'll use symbolic python
import sympy as sp
# we need to tell it which symbols to use
q1,q2 = sp.symbols('q1 q2')
q1

$\displaystyle q_{1}$

# sympy can take the derivative for us
c1 = "10 * q1 + 5 * q2"
s_mcost_1_q1 = sp.diff(c1 , q1)
s_mcost_1_q2 = sp.diff(c1 , q2)
print(s_mcost_1_q1,s_mcost_1_q2)

10 5

# and we can convert that to a function
mcost_1_q1 = sp.lambdify(q1,s_mcost_1_q1)
mcost_1_q2 = sp.lambdify(q2,s_mcost_1_q2)
mcost_1_q1(100),mcost_1_q2(100)

(10, 5)

Firm 1

# marginal cost 
cost_frame_1["Marginal Cost q1"] = np.vectorize(mcost_1_q1)(cost_frame_1['q1'])
cost_frame_1["Marginal Cost q2"] = np.vectorize(mcost_1_q2)(cost_frame_1['q2'])
cost_frame_1

	q1	q2	Total Cost	Average Cost q1	Average Cost q2	Marginal Cost q1	Marginal Cost q2	Incremental Cost q1	Incremental Cost q2
0	100	50	1250	10.0	5.0	10	5	10	5
1	60	50	850	10.0	5.0	10	5	10	5
2	40	50	650	10.0	5.0	10	5	10	5
3	30	10	350	10.0	5.0	10	5	10	5
4	30	50	550	10.0	5.0	10	5	10	5
5	30	70	650	10.0	5.0	10	5	10	5

Firm 2

q1,q2 = sp.symbols('q1 q2')
# sympy can take the derivative for us
c2 = "6 * q1 + q1**2 + 8 * q2 + q2**2"
s_mcost_2_q1 = sp.diff(c2 , q1)
s_mcost_2_q2 = sp.diff(c2 , q2)
print(s_mcost_2_q1,s_mcost_2_q2)
# and we can convert that to a function
mcost_2_q1 = sp.lambdify(q1,s_mcost_2_q1)
mcost_2_q2 = sp.lambdify(q2,s_mcost_2_q2)
mcost_2_q1(100),mcost_2_q2(50)

2*q1 + 6 2*q2 + 8

(206, 108)

# marginal cost 
cost_frame_2["Marginal Cost q1"] = np.vectorize(mcost_2_q1)(cost_frame_2['q1'])
cost_frame_2["Marginal Cost q2"] = np.vectorize(mcost_2_q2)(cost_frame_2['q2'])
cost_frame_2

	q1	q2	Total Cost	Average Cost q1	Average Cost q2	Marginal Cost q1	Marginal Cost q2
0	100	50	13500	106.0	58.0	206	108
1	60	50	6860	66.0	58.0	126	108
2	40	50	4740	46.0	58.0	86	108
3	30	10	1260	36.0	18.0	66	28
4	30	50	3980	36.0	58.0	66	108
5	30	70	6540	36.0	78.0	66	148

Firm 3

q1,q2 = sp.symbols('q1 q2')
# sympy can take the derivative for us
c3 = "7*q1 + 9*q2 + q1*q2"
s_mcost_3_q1 = sp.diff(c3 , q1)
s_mcost_3_q2 = sp.diff(c3 , q2)
print(s_mcost_3_q1,s_mcost_3_q2)
# and we can convert that to a function
# note tht we flip the inputs to match the function
mcost_3_q1 = sp.lambdify(q2,s_mcost_3_q1)
mcost_3_q2 = sp.lambdify(q1,s_mcost_3_q2)
mcost_3_q1(50),mcost_3_q2(100)

q2 + 7 q1 + 9

(57, 109)

# marginal cost 
cost_frame_3["Marginal Cost q1"] = np.vectorize(mcost_3_q1)(cost_frame_3['q2'])
cost_frame_3["Marginal Cost q2"] = np.vectorize(mcost_3_q2)(cost_frame_3['q1'])
cost_frame_3

	q1	q2	Total Cost	Marginal Cost q1	Marginal Cost q2
0	100	50	6150	57	109
1	60	50	3870	57	69
2	40	50	2730	57	49
3	30	10	600	17	39
4	30	50	2160	57	39
5	30	70	2940	77	39

Incremental Cost

$$IC(q_1) = C(q_1+1, q_2) - C(q_1,q_2)$$$$IC(q_2) = C(q_1, q_2+1) - C(q_1,q_2)$$

Which I find a little easier to write than to say :)

In python we'll just write a little function for this

# incremental cost if the cost of making the next unit by product
def inc_cost(cost_function,q1=q1,q2=q2,increment=str):
    '''
    cost_function: total cost function that you'd like to increment (over q1,q2)
    q1: the quantity you'd like to pass to the cost func as q1, defaults q1
    q2: same, default q2
    increment: the quantity you'd like to increment
    '''
    C_0 = cost_function(q1,q2)
    if increment == "q1":
        q1=q1+1
    elif increment == "q2":
        q2=q2+1
    else:
        print("increment must be one of q1,q2")
        return None
    C_1 = cost_function(q1,q2)
    return C_1 - C_0

Firm 1

# Incremental cost
cost_frame_1["Incremental Cost q1"] = np.vectorize(inc_cost)(
                                    cost_1,
                                    cost_frame_1['q1'],
                                    cost_frame_1['q2'],
                                    increment="q1"
                                    )
cost_frame_1["Incremental Cost q2"] = np.vectorize(inc_cost)(
                                    cost_1,
                                    cost_frame_1['q1'],
                                    cost_frame_1['q2'],
                                    increment="q2"
                                    )
cost_frame_1

	q1	q2	Total Cost	Average Cost q1	Average Cost q2	Marginal Cost q1	Marginal Cost q2	Incremental Cost q1	Incremental Cost q2
0	100	50	1250	10.0	5.0	10	5	10	5
1	60	50	850	10.0	5.0	10	5	10	5
2	40	50	650	10.0	5.0	10	5	10	5
3	30	10	350	10.0	5.0	10	5	10	5
4	30	50	550	10.0	5.0	10	5	10	5
5	30	70	650	10.0	5.0	10	5	10	5

Firm 2

# Incremental cost
cost_frame_2["Incremental Cost q1"] = np.vectorize(inc_cost)(
                                    cost_2,
                                    cost_frame_2['q1'],
                                    cost_frame_2['q2'],
                                    increment="q1"
                                    )
cost_frame_2["Incremental Cost q2"] = np.vectorize(inc_cost)(
                                    cost_2,
                                    cost_frame_2['q1'],
                                    cost_frame_2['q2'],
                                    increment="q2"
                                    )
cost_frame_2

	q1	q2	Total Cost	Average Cost q1	Average Cost q2	Marginal Cost q1	Marginal Cost q2	Incremental Cost q1	Incremental Cost q2
0	100	50	13500	106.0	58.0	206	108	207	109
1	60	50	6860	66.0	58.0	126	108	127	109
2	40	50	4740	46.0	58.0	86	108	87	109
3	30	10	1260	36.0	18.0	66	28	67	29
4	30	50	3980	36.0	58.0	66	108	67	109
5	30	70	6540	36.0	78.0	66	148	67	149

Firm 3

# Incremental cost
cost_frame_3["Incremental Cost q1"] = np.vectorize(inc_cost)(
                                    cost_3,
                                    cost_frame_3['q1'],
                                    cost_frame_3['q2'],
                                    increment="q1"
                                    )
cost_frame_3["Incremental Cost q2"] = np.vectorize(inc_cost)(
                                    cost_3,
                                    cost_frame_3['q1'],
                                    cost_frame_3['q2'],
                                    increment="q2"
                                    )
cost_frame_3

	q1	q2	Total Cost	Marginal Cost q1	Marginal Cost q2	Incremental Cost q1	Incremental Cost q2
0	100	50	6150	57	109	57	109
1	60	50	3870	57	69	57	69
2	40	50	2730	57	49	57	49
3	30	10	600	17	39	17	39
4	30	50	2160	57	39	57	39
5	30	70	2940	77	39	77	39

Let's make a 3d graph in Python!!!

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np # we already have np 
q1

$\displaystyle q_{1}$

# Create data for the plot
q1 = np.linspace(0, 1_000, 1_000)
q2 = np.linspace(0, 1_000, 1_000)
Q1, Q2 = np.meshgrid(q1, q2)
# calc costs
C1 = 10 * Q1 + 5 * Q2 
C2 = 6 * Q1 + Q1**2 + 8 * Q2 + Q2**2
C3 = 7 * Q1 + 9 * Q2 + Q1 * Q2    

# Create the figure and add a 3D axis
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Plot the data
# ax.plot_surface(Q1, Q2, C1)
# ax.plot_surface(Q1, Q2, C2)
ax.plot_surface(Q1, Q2, C3)

# Set axis labels and show the plot
ax.set_xlabel('Q1')
ax.set_ylabel('Q2')
ax.set_zlabel('Cost')
plt.show()